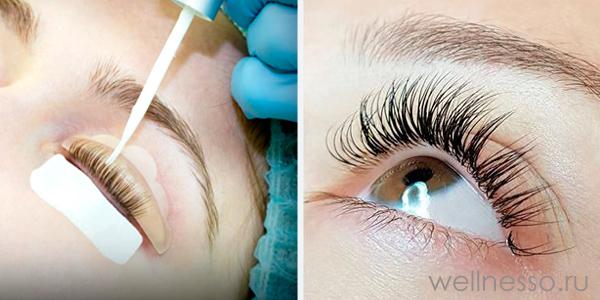
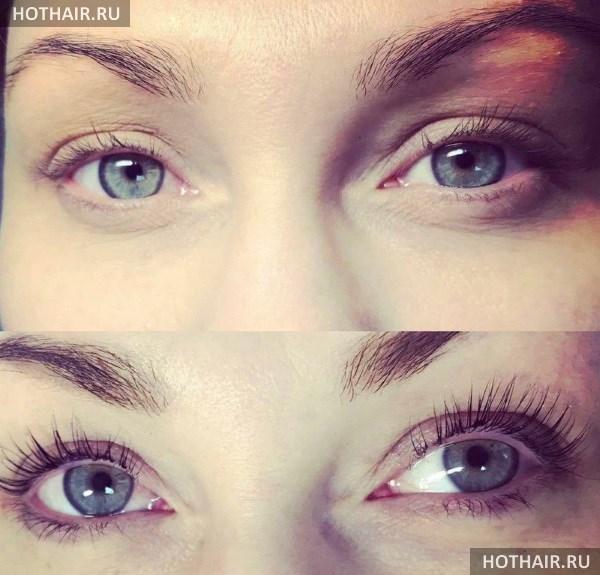
Изгибы ресниц при наращивании
Определение слова Изгиб по БСЭ
Изгиб — в сопротивлении материалов, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого объекта (бруса, балки, плиты, оболочки и др.) под действием внешних сил или температуры. Применительно к прямому брусу различают И.: простой, или плоский, при котором внешние силы лежат в одной из главных плоскостей бруса (т. е. плоскостей, проходящих через его ось и главные оси инерции поперечного сечения) (см. Моменты инерции). сложный, вызываемый силами, расположенными в разных плоскостях. косой, являющийся частным случаем сложного И. (см. Косой изгиб). В зависимости от действующих в поперечном сечении бруса силовых факторов (рис. 1, а, б) И. называется чистым (при наличии только изгибающих моментов) и поперечным (при наличии также и поперечных сил). В инженерной практике рассматривается также особый случай И. — продольный И. (рис. 1, в), характеризующийся выпучиванием стержня под действием продольных сжимающих сил (см. Продольный изгиб). Одновременное действие сил, направленных по оси стержня и перпендикулярно к ней, вызывает продольно-поперечный И. (рис. 1, г).Приближённый расчёт прямого бруса на действие И. в упругой стадии производится в предположении, что поперечные сечения бруса, плоские до И., остаются плоскими и после него (гипотеза плоских сечений). полагают также, что продольные волокна бруса при И. не давят друг на друга и не стремятся оторваться одно от другого. При плоском И. в поперечных сечениях бруса возникают нормальные и касательные напряжения. Нормальные напряжения &sigma. в произвольном волокне какого-либо поперечного сечения бруса (рис. 2), лежащем на расстоянии y от нейтральной оси, определяются формулой &sigma. = Mzy &frasl. Iz, где Mz — изгибающий момент в сечении, а Iz — момент инерции поперечного сечения относительно нейтральной оси.Наибольшие нормальные напряжения возникают в крайних волокнах сечения
| &sigma.max = | Mz&mdash.&mdash.Wz | (Wz = | Iz&mdash.&mdash.ymax | &ndash. |
Касательные
| &tau. = | Qy Sz&mdash.&mdash.&mdash.Iz b | , |
yпоперечнаяzширинаХарактеризмененияобычнозначениякривизна
| 1&mdash.&rho. | = | Mz&mdash.&mdash.E Iz | , |
радиусмодульмалыхприближённовторойпроизводнойпоэтомумеждуизогнутоймоментом
| dІV&mdash.&mdash.dxІ | = | Mz&mdash.&mdash.E Iz | , |
уравнениялиниявозрастаниинагрузкипервоначальнозатемпластическиеРаспределениесостояниитекучеститнеограниченнопрт1212растянутойприСопротивлениеЧистыйэлемент